Category Theory Presentation
Yesterday I was happy to make a presentation about Category Theory at Riviera Scala Clojure Meetup (note I used only Haskell for my examples).
- Click here to go to the HTML presentation.
- Click Here to download the PDF slides (LaTeX not rendered properly)
If you don't want to read them through an HTML presentations framework or downloading a big PDF just continue to read as a standard web page.
Category Theory & Programming
Plan
- General overview
- Definitions
- Applications
Not really about: Cat & glory

General Overview


Recent Math Field
1942-45, Samuel Eilenberg & Saunders Mac Lane
Certainly one of the more abstract branches of math
- New math foundation
formalism abstraction, package entire theory★ - Bridge between disciplines
Physics, Quantum Physics, Topology, Logic, Computer Science☆
★: When is one thing equal to some other thing?, Barry Mazur, 2007
☆: Physics, Topology, Logic and Computation: A Rosetta Stone, John C. Baez, Mike Stay, 2009
From a Programmer perspective
Category Theory is a new language/framework for Math
- Another way of thinking
- Extremely efficient for generalization
Math Programming relation
Programming is doing Math
Strong relations between type theory and category theory.
Not convinced?
Certainly a vocabulary problem.
One of the goal of Category Theory is to create a homogeneous vocabulary between different disciplines.
Vocabulary

Math vocabulary used in this presentation:
Category, Morphism, Associativity, Preorder, Functor, Endofunctor, Categorial property, Commutative diagram, Isomorph, Initial, Dual, Monoid, Natural transformation, Monad, Klesli arrows, κατα-morphism, ...
Programmer Translation

| Mathematician | Programmer |
|---|---|
| Morphism | Arrow |
| Monoid | String-like |
| Preorder | Acyclic graph |
| Isomorph | The same |
| Natural transformation | rearrangement function |
| Funny Category | LOLCat |
Plan
- General overview
- Definitions
- Category
- Intuition
- Examples
- Functor
- Examples
- Applications
Category
A way of representing things and ways to go between things.
A Category \(\mathcal{C}\) is defined by:
- Objects \(\ob{C}\),
- Morphisms \(\hom{C}\),
- a Composition law (∘)
- obeying some Properties.
Category: Objects
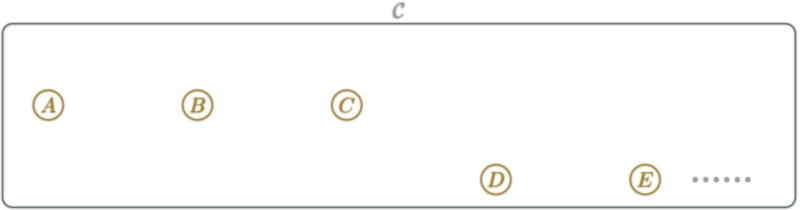
\(\ob{\mathcal{C}}\) is a collection
Category: Morphisms
\(A\) and \(B\) objects of \(\C\)
\(\hom{A,B}\) is a collection of morphisms
\(f:A→B\) denote the fact \(f\) belongs to \(\hom{A,B}\)
\(\hom{\C}\) the collection of all morphisms of \(\C\)
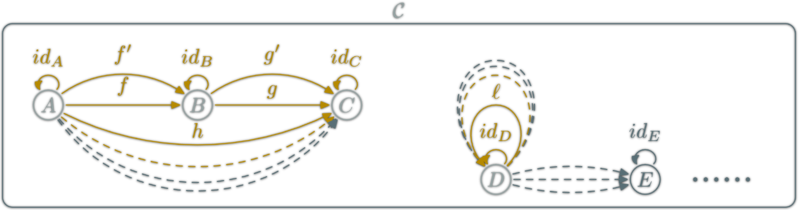
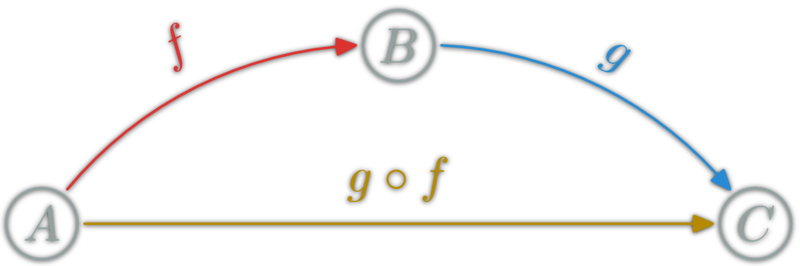
Category: Composition
Composition (∘): associate to each couple \(f:A→B, g:B→C\) $$g∘f:A\rightarrow C$$
Category laws: neutral element
for each object \(X\), there is an \(\id_X:X→X\),
such that for each \(f:A→B\):
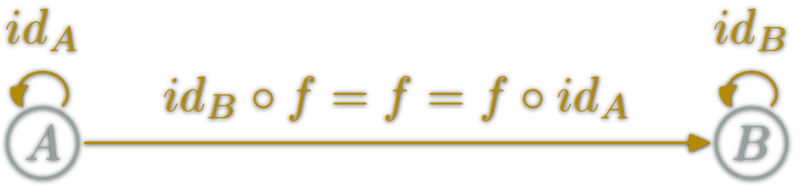
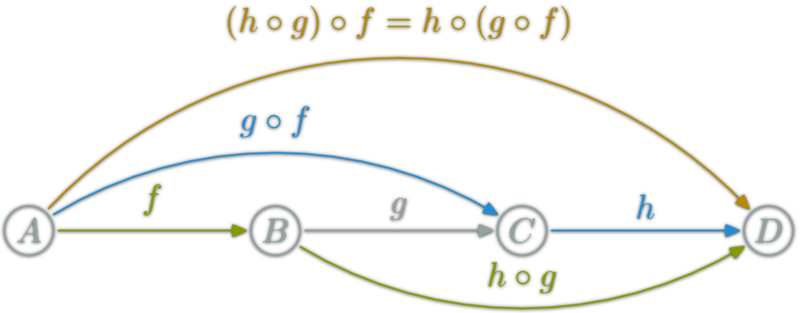
Category laws: Associativity
Composition is associative:
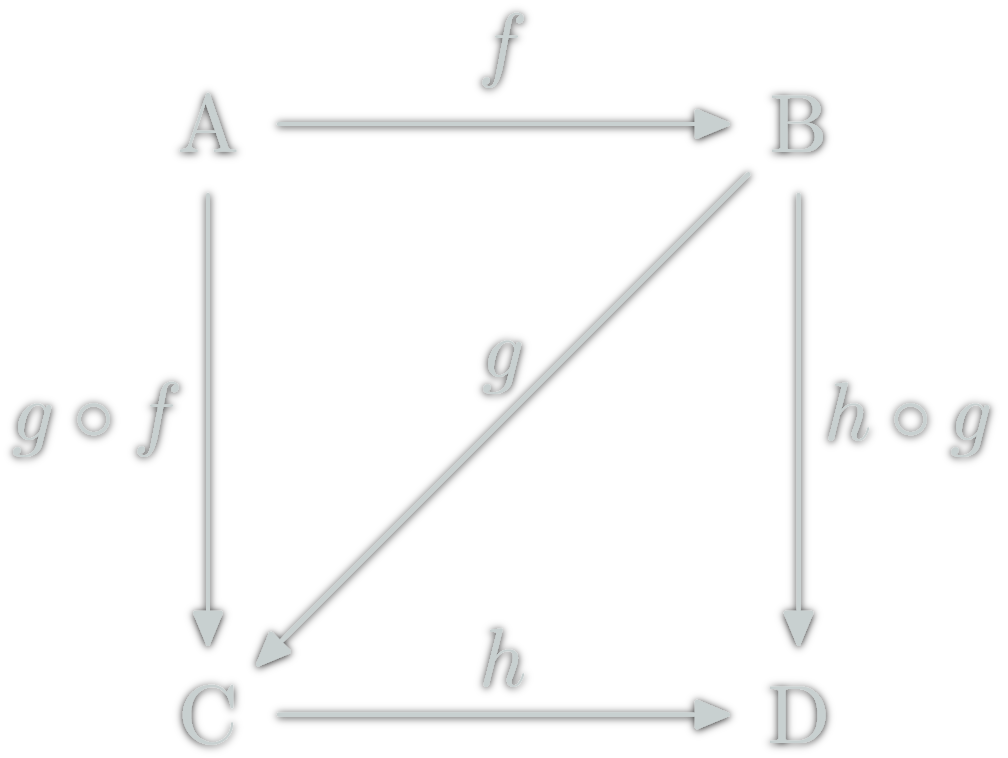
Commutative diagrams
Two path with the same source and destination are equal.
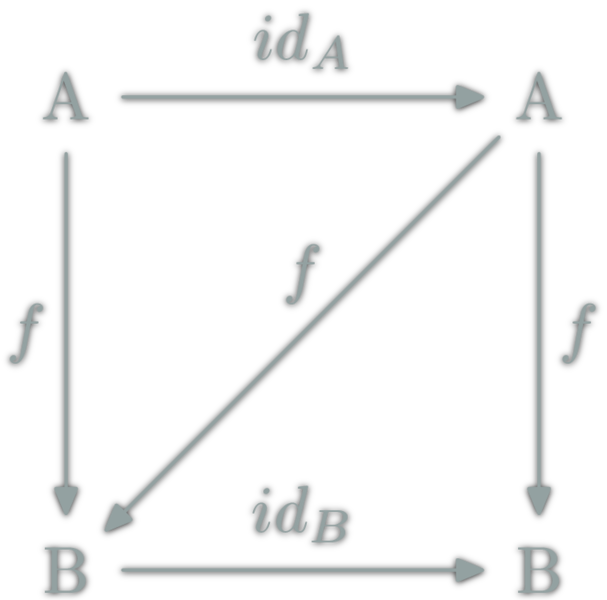
Question Time!

Can this be a category?
\(\ob{\C},\hom{\C}\) fixed, is there a valid ∘?
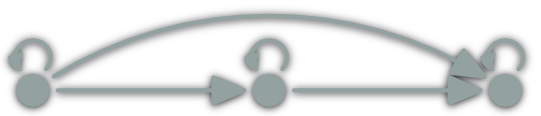

NO
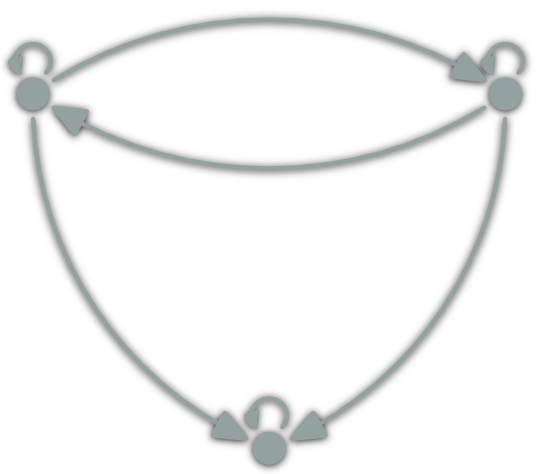
Can this be a category?
NO
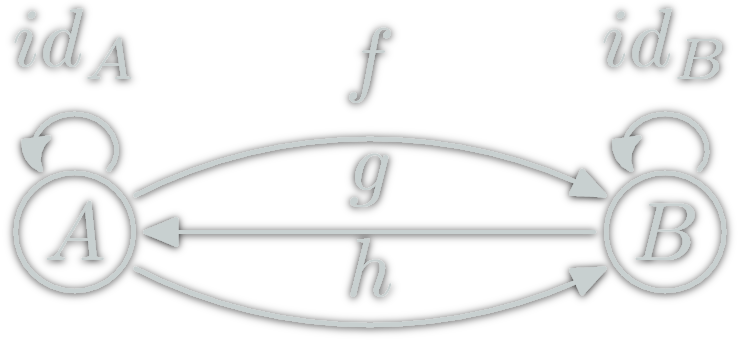
\(h∘(g∘f)=h∘\id_A=h\)
but \(h≠f\)
NO
Categories Examples

Category \(\Set\)
- \(\ob{\Set}\) are all the sets
- \(\hom{E,F}\) are all functions from \(E\) to \(F\)
- ∘ is functions composition
- \(\ob{\Set}\) is a proper class ; not a set
- \(\hom{E,F}\) is a set
- \(\Set\) is then a locally small category
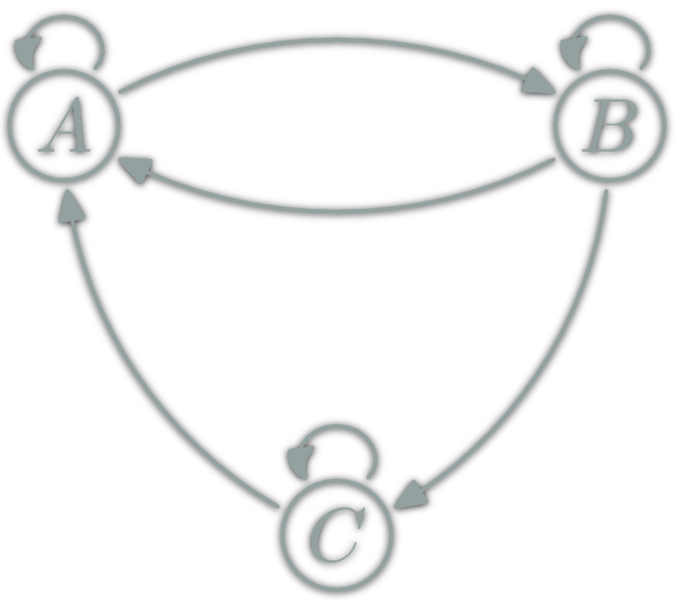
Categories Everywhere?

- \(\Mon\): (monoids, monoid morphisms,∘)
- \(\Vec\): (Vectorial spaces, linear functions,∘)
- \(\Grp\): (groups, group morphisms,∘)
- \(\Rng\): (rings, ring morphisms,∘)
- Any deductive system T: (theorems, proofs, proof concatenation)
- \( \Hask\): (Haskell types, functions,
(.)) - ...
Smaller Examples
Strings
- \(\ob{Str}\) is a singleton
- \(\hom{Str}\) each string
- ∘ is concatenation
(++)
-
"" ++ u = u = u ++ "" -
(u ++ v) ++ w = u ++ (v ++ w)
Finite Example?
Graph
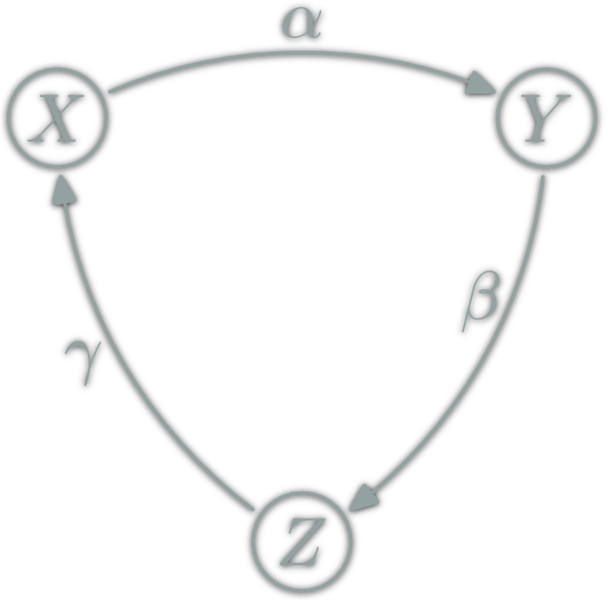
- \(\ob{G}\) are vertices
- \(\hom{G}\) each path
- ∘ is path concatenation
- \(\ob{G}=\{X,Y,Z\}\),
- \(\hom{G}=\{ε,α,β,γ,αβ,βγ,...\}\)
- \(αβ∘γ=αβγ\)
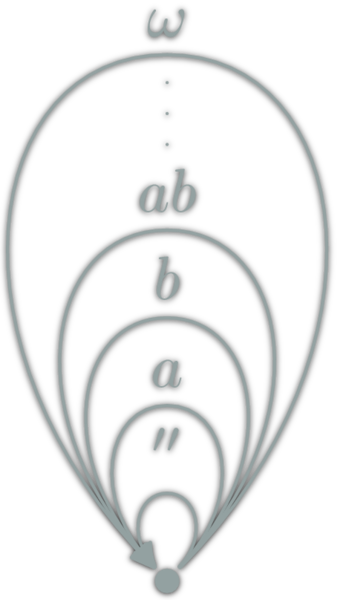
Number construction
Each Numbers as a whole category
Degenerated Categories: Monoids
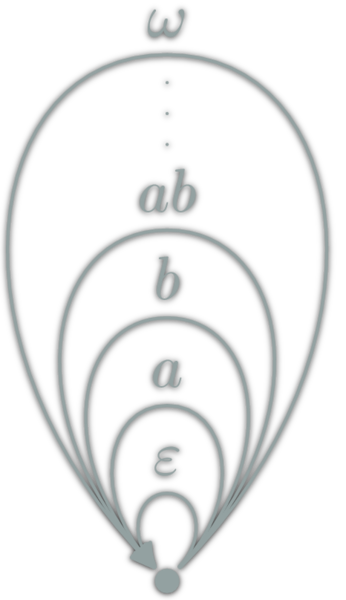
Each Monoid \((M,e,⊙): \ob{M}=\{∙\},\hom{M}=M,\circ = ⊙\)
Only one object.
Examples:
(Integer,0,+),(Integer,1,*),(Strings,"",++), for eacha,([a],[],++)
Degenerated Categories: Preorders \((P,≤)\)
- \(\ob{P}={P}\),
- \(\hom{x,y}=\{x≤y\} ⇔ x≤y\),
- \((y≤z) \circ (x≤y) = (x≤z) \)
At most one morphism between two objects.

Degenerated Categories: Discrete Categories
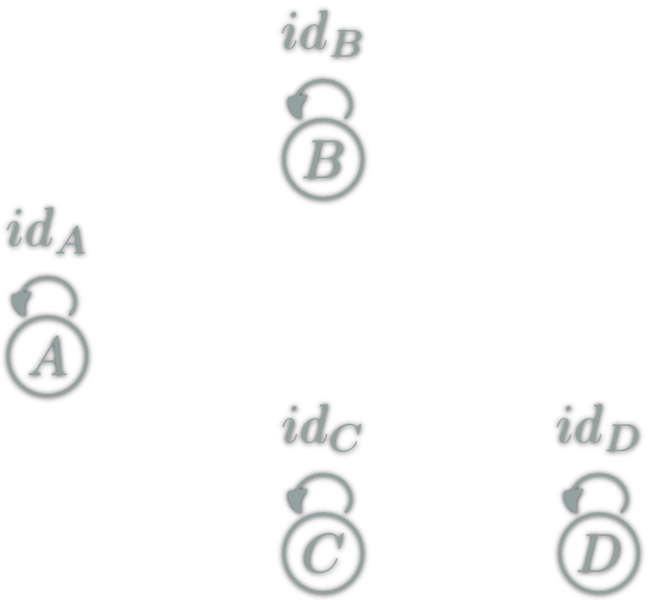
Any Set
Any set \(E: \ob{E}=E, \hom{x,y}=\{x\} ⇔ x=y \)
Only identities
Choice
The same object can be seen in many different way as a category.
You can choose what are object, morphisms and composition.
ex: Str and discrete(Σ*)
Categorical Properties
Any property which can be expressed in term of category, objects, morphism and composition.
- Dual: \(\D\) is \(\C\) with reversed morphisms.
- Initial: \(Z\in\ob{\C}\) s.t. \(∀Y∈\ob{\C}, \#\hom{Z,Y}=1\)
Unique ("up to isormophism") - Terminal: \(T\in\ob{\C}\) s.t. \(T\) is initial in the dual of \(\C\)
- Functor: structure preserving mapping between categories
- ...
Isomorph
 isomorphism: \(f:A→B\) which can be "undone" i.e.
isomorphism: \(f:A→B\) which can be "undone" i.e.
\(∃g:B→A\), \(g∘f=id_A\) & \(f∘g=id_B\)
in this case, \(A\) & \(B\) are isomorphic.
A≌B means A and B are essentially the same.
In Category Theory, = is in fact mostly ≌.
For example in commutative diagrams.
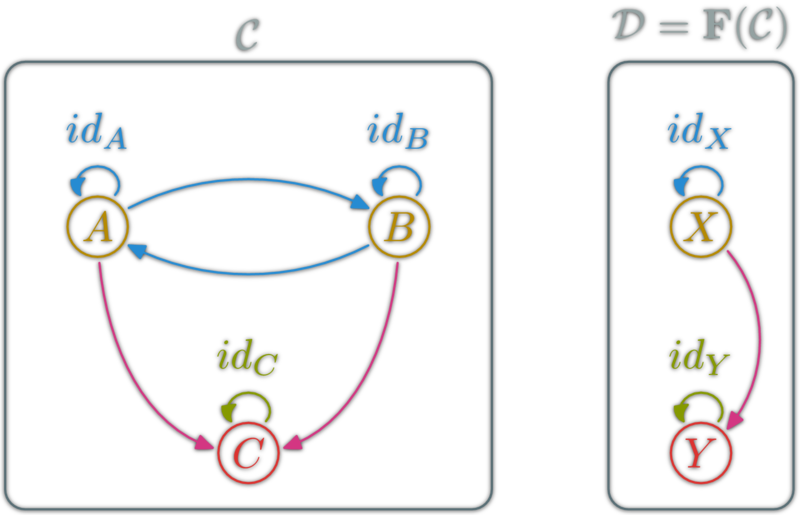
Functor
A functor is a mapping between two categories. Let \(\C\) and \(\D\) be two categories. A functor \(\F\) from \(\C\) to \(\D\):
- Associate objects: \(A\in\ob{\C}\) to \(\F(A)\in\ob{\D}\)
- Associate morphisms: \(f:A\to B\) to \(\F(f) : \F(A) \to \F(B)\)
such that
- \( \F (\)\(\id_X\)\()= \)\(\id\)\(\vphantom{\id}_{\F(}\)\(\vphantom{\id}_X\)\(\vphantom{\id}_{)} \),
- \( \F (\)\(g∘f\)\()= \)\( \F(\)\(g\)\() \)\(\circ\)\( \F(\)\(f\)\() \)
Functor Example (ob → ob)
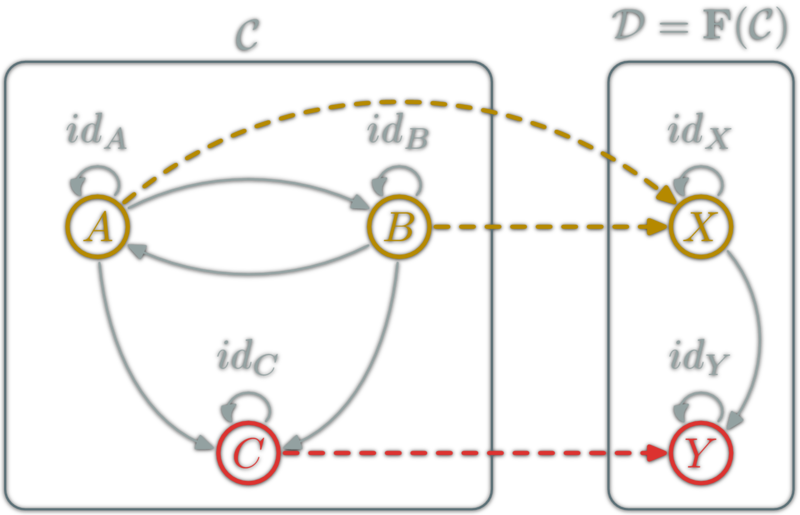
Functor Example (hom → hom)
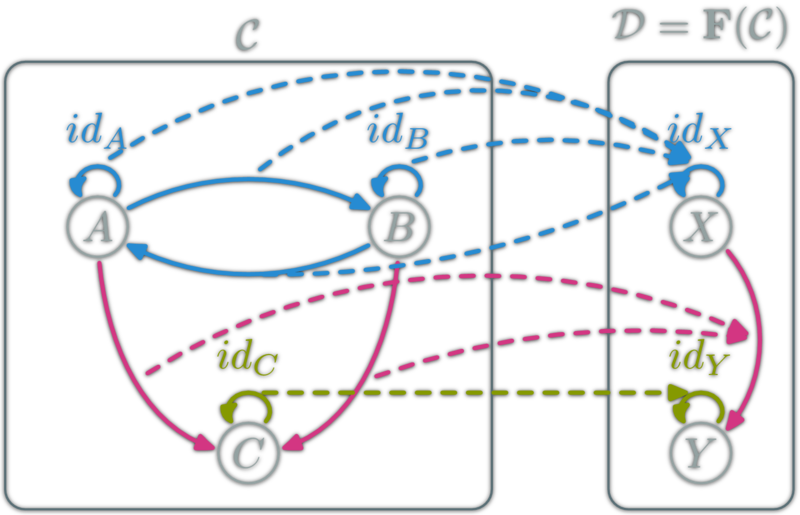
Functor Example
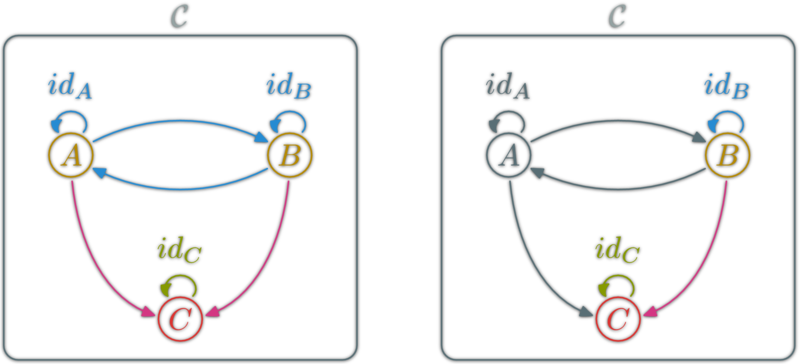
Endofunctors
An endofunctor for \(\C\) is a functor \(F:\C→\C\).
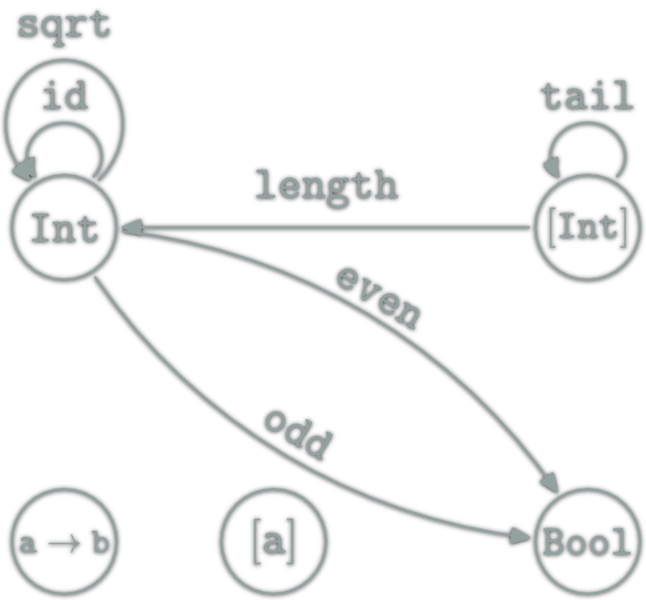
Category of Categories

Categories and functors form a category: \(\Cat\)
- \(\ob{\Cat}\) are categories
- \(\hom{\Cat}\) are functors
- ∘ is functor composition
Plan
- General overview
- Definitions
- Applications
- \(\Hask\) category
- Functors
- Natural transformations
- Monads
- κατα-morphisms
Hask
Category \(\Hask\):
- \(\ob{\Hask} = \) Haskell types
- \(\hom{\Hask} = \) Haskell functions
-
∘ =
(.)Haskell function composition
Forget glitches because of undefined.
Haskell Kinds
In Haskell some types can take type variable(s). Typically: [a].
Types have kinds; The kind is to type what type is to function. Kind are the types for types (so meta).
Int, Char :: *
[], Maybe :: * -> *
(,), (->) :: * -> * -> *
[Int], Maybe Char, Maybe [Int] :: *Haskell Types
Sometimes, the type determine a lot about the function★:
fst :: (a,b) -> a -- Only one choice
snd :: (a,b) -> b -- Only one choice
f :: a -> [a] -- Many choices
-- Possibilities: f x=[], or [x], or [x,x] or [x,...,x]
? :: [a] -> [a] -- Many choices
-- can only rearrange: duplicate/remove/reorder elements
-- for example: the type of addOne isn't [a] -> [a]
addOne l = map (+1) l
-- The (+1) force 'a' to be a Num.
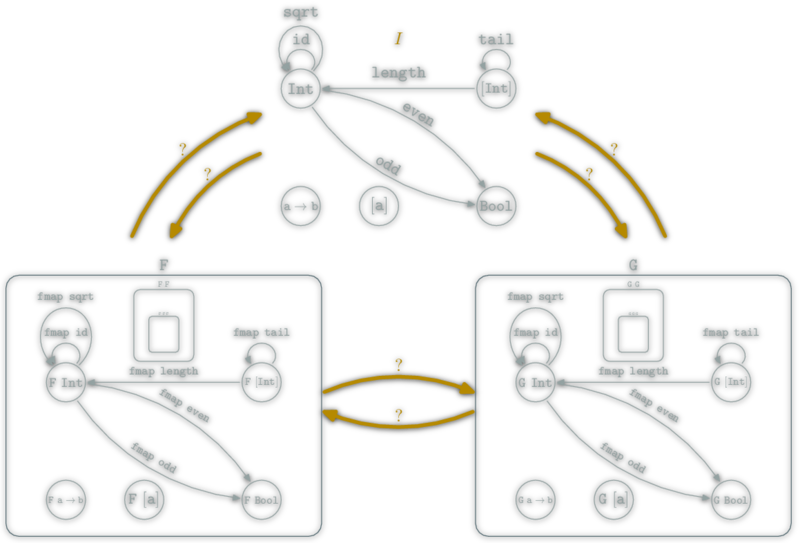
Haskell Functor vs \(\Hask\) Functor
A Haskell Functor is a type F :: * -> * which belong to the type class Functor ; thus instantiate
fmap :: (a -> b) -> (F a -> F b).
& F: \(\ob{\Hask}→\ob{\Hask}\)
& fmap: \(\hom{\Hask}→\hom{\Hask}\)
The couple (F,fmap) is a \(\Hask\)'s functor if for any x :: F a:
fmap id x = xfmap (f.g) x= (fmap f . fmap g) x
Haskell Functors Example: Maybe
data Maybe a = Just a | Nothing
instance Functor Maybe where
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap f (Just a) = Just (f a)
fmap f Nothing = Nothingfmap (+1) (Just 1) == Just 2
fmap (+1) Nothing == Nothing
fmap head (Just [1,2,3]) == Just 1Haskell Functors Example: List
instance Functor ([]) where
fmap :: (a -> b) -> [a] -> [b]
fmap = mapfmap (+1) [1,2,3] == [2,3,4]
fmap (+1) [] == []
fmap head [[1,2,3],[4,5,6]] == [1,4]Haskell Functors for the programmer
Functor is a type class used for types that can be mapped over.
- Containers:
[], Trees, Map, HashMap... - "Feature Type":
Maybe a: help to handle absence ofa.
Ex:safeDiv x 0 ⇒ NothingEither String a: help to handle errors
Ex:reportDiv x 0 ⇒ Left "Division by 0!"
Haskell Functor intuition
Put normal function inside a container. Ex: list, trees...
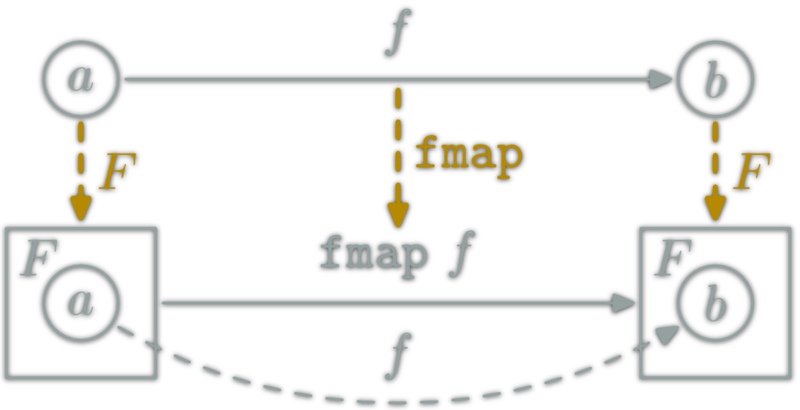
Haskell Functor properties
Haskell Functors are:
- endofunctors ; \(F:\C→\C\) here \(\C = \Hask\),
- a couple (Object,Morphism) in \(\Hask\).
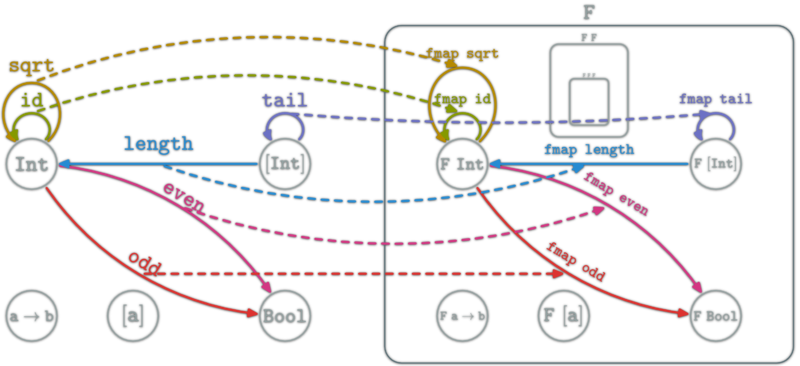
Functor as boxes
Haskell functor can be seen as boxes containing all Haskell types and functions. Haskell types look like a fractal:
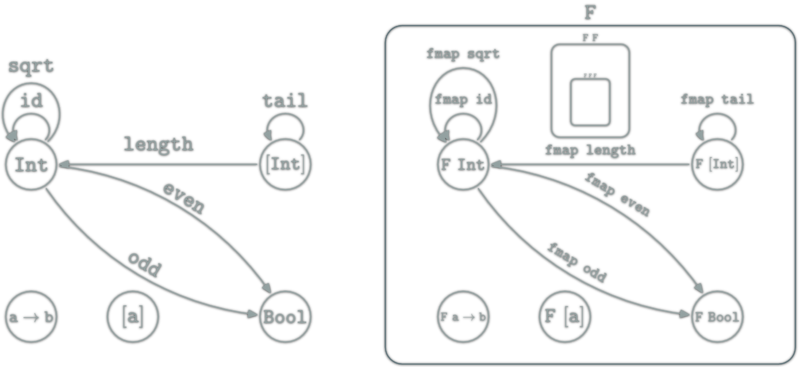
Functor as boxes
Haskell functor can be seen as boxes containing all Haskell types and functions. Haskell types look like a fractal:
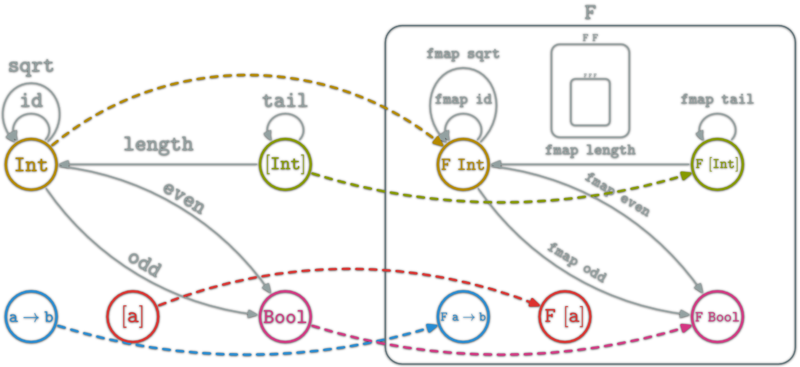
Functor as boxes
Haskell functor can be seen as boxes containing all Haskell types and functions. Haskell types look like a fractal:
"Non Haskell" Hask's Functors
A simple basic example is the \(id_\Hask\) functor. It simply cannot be expressed as a couple (F,fmap) where
F::* -> *fmap :: (a -> b) -> (F a) -> (F b)
Another example:
- F(
T)=Int - F(
f)=\_->0
Also Functor inside \(\Hask\)
\(\mathtt{[a]}∈\ob{\Hask}\) but is also a category. Idem for Int.
length is a Functor from the category [a] to the category Int:
- \(\ob{\mathtt{[a]}}=\{∙\}\)
- \(\hom{\mathtt{[a]}}=\mathtt{[a]}\)
- \(∘=\mathtt{(++)}\)
⇒
- \(\ob{\mathtt{Int}}=\{∙\}\)
- \(\hom{\mathtt{Int}}=\mathtt{Int}\)
- \(∘=\mathtt{(+)}\)
- id:
length [] = 0 - comp:
length (l ++ l') = (length l) + (length l')
Category of \(\Hask\) Endofunctors

Category of Functors
If \(\C\) is small (\(\hom{\C}\) is a set). All functors from \(\C\) to some category \(\D\) form the category \(\mathrm{Func}(\C,\D)\).
- \(\ob{\mathrm{Func}(\C,\D)}\): Functors \(F:\C→\D\)
- \(\hom{\mathrm{Func}(\C,\D)}\): natural transformations
- ∘: Functor composition
\(\mathrm{Func}(\C,\C)\) is the category of endofunctors of \(\C\).
Natural Transformations
Let \(F\) and \(G\) be two functors from \(\C\) to \(\D\).
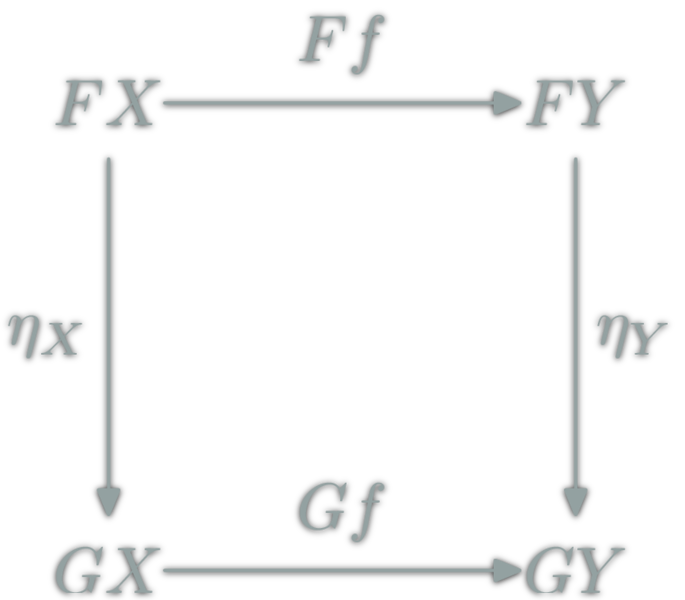 A natural transformation: familly η ; \(η_X\in\hom{\D}\) for \(X\in\ob{\C}\) s.t.
A natural transformation: familly η ; \(η_X\in\hom{\D}\) for \(X\in\ob{\C}\) s.t.
ex: between Haskell functors; F a -> G a
Rearragement functions only.
Natural Transformation Examples (1/4)
data List a = Nil | Cons a (List a)
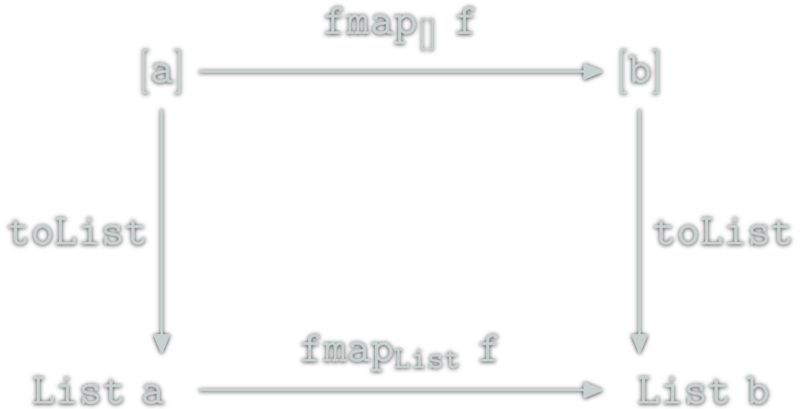
toList :: [a] -> List a
toList [] = Nil
toList (x:xs) = Cons x (toList xs)toList is a natural transformation. It is also a morphism from [] to List in the Category of \(\Hask\) endofunctors.

Natural Transformation Examples (2/4)
data List a = Nil | Cons a (List a)
toHList :: List a -> [a]
toHList Nil = []
toHList (Cons x xs) = x:toHList xstoHList is a natural transformation. It is also a morphism from List to [] in the Category of \(\Hask\) endofunctors.
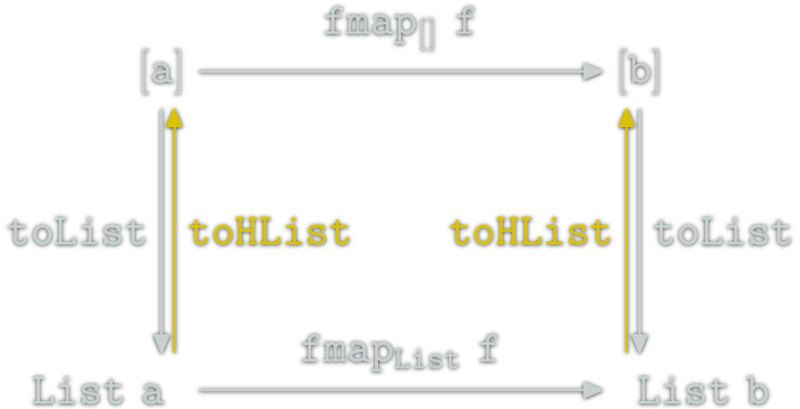

toList . toHList = id & toHList . toList = id &therefore
[] & List are isomorph. Natural Transformation Examples (3/4)
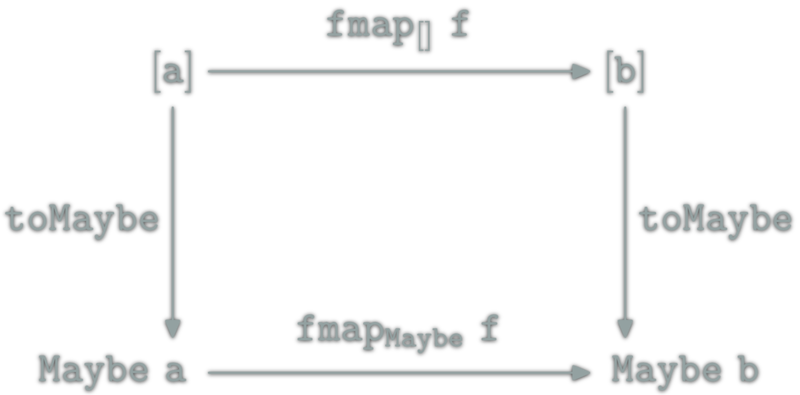
toMaybe :: [a] -> Maybe a
toMaybe [] = Nothing
toMaybe (x:xs) = Just xtoMaybe is a natural transformation. It is also a morphism from [] to Maybe in the Category of \(\Hask\) endofunctors.

Natural Transformation Examples (4/4)
mToList :: Maybe a -> [a]
mToList Nothing = []
mToList Just x = [x]toMaybe is a natural transformation. It is also a morphism from [] to Maybe in the Category of \(\Hask\) endofunctors.
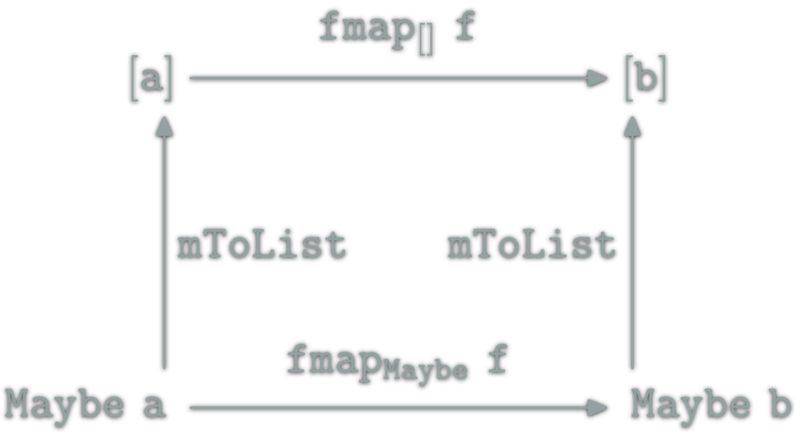
![relation between [] and Maybe](http://yogsototh.github.io/Category-Theory-Presentation/categories/img/mp/maybe-list-endofunctor-morphsm.png)
Hint:
Bool lists longer than 1. Composition problem
The Problem; example with lists:
f x = [x] ⇒ f 1 = [1] ⇒ (f.f) 1 = [[1]] ✗
g x = [x+1] ⇒ g 1 = [2] ⇒ (g.g) 1 = ERROR [2]+1 ✗
h x = [x+1,x*3] ⇒ h 1 = [2,3] ⇒ (h.h) 1 = ERROR [2,3]+1 ✗ The same problem with most f :: a -> F a functions and functor F.
Composition Fixable?
How to fix that? We want to construct an operator which is able to compose:
f :: a -> F b & g :: b -> F c.
More specifically we want to create an operator ◎ of type
◎ :: (b -> F c) -> (a -> F b) -> (a -> F c)
Note: if F = I, ◎ = (.).
Fix Composition (1/2)
Goal, find: ◎ :: (b -> F c) -> (a -> F b) -> (a -> F c)f :: a -> F b, g :: b -> F c:
(g ◎ f) x???- First apply
ftox⇒f x :: F b - Then how to apply
gproperly to an element of typeF b?
Fix Composition (2/2)
Goal, find: ◎ :: (b -> F c) -> (a -> F b) -> (a -> F c)f :: a -> F b, g :: b -> F c, f x :: F b:
- Use
fmap :: (t -> u) -> (F t -> F u)! (fmap g) :: F b -> F (F c); (t=b,u=F c)(fmap g) (f x) :: F (F c)it almost WORKS!- We lack an important component,
join :: F (F c) -> F c (g ◎ f) x = join ((fmap g) (f x))☺
◎ is the Kleisli composition; in Haskell:<=<(inControl.Monad).
Necessary laws
For ◎ to work like composition, we need join to hold the following properties:
join (join (F (F (F a))))=join (F (join (F (F a))))- abusing notations denoting
joinby ⊙; this is equivalent to(F ⊙ F) ⊙ F = F ⊙ (F ⊙ F) - There exists
η :: a -> F as.t.η⊙F=F=F⊙η
Klesli composition
Now the composition works as expected. In Haskell ◎ is <=< in Control.Monad.
g <=< f = \x -> join ((fmap g) (f x))
f x = [x] ⇒ f 1 = [1] ⇒ (f <=< f) 1 = [1] ✓
g x = [x+1] ⇒ g 1 = [2] ⇒ (g <=< g) 1 = [3] ✓
h x = [x+1,x*3] ⇒ h 1 = [2,3] ⇒ (h <=< h) 1 = [3,6,4,9] ✓We reinvented Monads!
A monad is a triplet (M,⊙,η) where
- \(M\) an Endofunctor (to type
aassociateM a) - \(⊙:M×M→M\) a nat. trans. (i.e.
⊙::M (M a) → M a;join) - \(η:I→M\) a nat. trans. (\(I\) identity functor ;
η::a → M a)
Satisfying
- \(M ⊙ (M ⊙ M) = (M ⊙ M) ⊙ M\)
- \(η ⊙ M = M = M ⊙ η\)
Compare with Monoid
A Monoid is a triplet \((E,∙,e)\) s.t.
- \(E\) a set
- \(∙:E×E→E\)
- \(e:1→E\)
Satisfying
- \(x∙(y∙z) = (x∙y)∙z, ∀x,y,z∈E\)
- \(e∙x = x = x∙e, ∀x∈E\)
Monads are just Monoids
A Monad is just a monoid in the category of endofunctors, what's the problem?
The real sentence was:
All told, a monad in X is just a monoid in the category of endofunctors of X, with product × replaced by composition of endofunctors and unit set by the identity endofunctor.
Example: List
[] :: * -> *an Endofunctor- \(⊙:M×M→M\) a nat. trans. (
join :: M (M a) -> M a) - \(η:I→M\) a nat. trans.
-- In Haskell ⊙ is "join" in "Control.Monad"
join :: [[a]] -> [a]
join = concat
-- In Haskell the "return" function (unfortunate name)
η :: a -> [a]
η x = [x]Example: List (law verification)
Example: List is a functor (join is ⊙)
- \(M ⊙ (M ⊙ M) = (M ⊙ M) ⊙ M\)
- \(η ⊙ M = M = M ⊙ η\)
join [ join [[x,y,...,z]] ] = join [[x,y,...,z]]
= join (join [[[x,y,...,z]]])
join (η [x]) = [x] = join [η x]Therefore ([],join,η) is a monad.
Monads useful?
A LOT of monad tutorial on the net. Just one example; the State Monad
DrawScene to State Screen DrawScene ; still pure.
main = drawImage (width,height)
drawImage :: Screen -> DrawScene
drawImage screen = do
drawPoint p screen
drawCircle c screen
drawRectangle r screen
drawPoint point screen = ...
drawCircle circle screen = ...
drawRectangle rectangle screen = ...main = do
put (Screen 1024 768)
drawImage
drawImage :: State Screen DrawScene
drawImage = do
drawPoint p
drawCircle c
drawRectangle r
drawPoint :: Point ->
State Screen DrawScene
drawPoint p = do
Screen width height <- get
...fold

κατα-morphism

κατα-morphism: fold generalization
acc type of the "accumulator":fold :: (acc -> a -> acc) -> acc -> [a] -> acc
Idea: put the accumulated value inside the type.
-- Equivalent to fold (+1) 0 "cata"
(Cons 'c' (Cons 'a' (Cons 't' (Cons 'a' Nil))))
(Cons 'c' (Cons 'a' (Cons 't' (Cons 'a' 0))))
(Cons 'c' (Cons 'a' (Cons 't' 1)))
(Cons 'c' (Cons 'a' 2))
(Cons 'c' 3)
4But where are all the informations? (+1) and 0?
κατα-morphism: Missing Information
Where is the missing information?
- Functor operator
fmap - Algebra representing the
(+1)and also knowing about the0.
First example, make length on [Char]
κατα-morphism: Type work
data StrF a = Cons Char a | Nil
data Str' = StrF Str'
-- generalize the construction of Str to other datatype
-- Mu: type fixed point
-- Mu :: (* -> *) -> *
data Mu f = InF { outF :: f (Mu f) }
data Str = Mu StrF
-- Example
foo=InF { outF = Cons 'f'
(InF { outF = Cons 'o'
(InF { outF = Cons 'o'
(InF { outF = Nil })})})}κατα-morphism: missing information retrieved
type Algebra f a = f a -> a
instance Functor (StrF a) =
fmap f (Cons c x) = Cons c (f x)
fmap _ Nil = Nilcata :: Functor f => Algebra f a -> Mu f -> a
cata f = f . fmap (cata f) . outFκατα-morphism: Finally length
All needed information for making length.
instance Functor (StrF a) =
fmap f (Cons c x) = Cons c (f x)
fmap _ Nil = Nil
length' :: Str -> Int
length' = cata phi where
phi :: Algebra StrF Int -- StrF Int -> Int
phi (Cons a b) = 1 + b
phi Nil = 0
main = do
l <- length' $ stringToStr "Toto"
...κατα-morphism: extension to Trees
Once you get the trick, it is easy to extent to most Functor.
type Tree = Mu TreeF
data TreeF x = Node Int [x]
instance Functor TreeF where
fmap f (Node e xs) = Node e (fmap f xs)
depth = cata phi where
phi :: Algebra TreeF Int -- TreeF Int -> Int
phi (Node x sons) = 1 + foldr max 0 sonsConclusion
Category Theory oriented Programming:
- Focus on the type and operators
- Extreme generalisation
- Better modularity
- Better control through properties of types
No cat were harmed in the making of this presentation.