Haskell Progressive Example

Introduction

In my preceding article I introduced Haskell.

This article goes further. It will show how to use functional programming with interactive programs. But more than that, it will show how to organize your code in a functional way. This article is more about functional paradigm than functional language. The code organization can be used in most imperative language.

As Haskell is designed for functional paradigm, it is easier to use in this context. In reality, the firsts sections will use an imperative paradigm. As you can use functional paradigm in imperative language, you can also use imperative paradigm in functional languages.

This article is about creating an useful and clean program. It can interact with the user in real time. It uses OpenGL, a library with imperative programming foundations. Despite this fact, most of the final code will remain in the pure part (no IO).

I believe the main audience for this article are:

• Haskell programmer looking for an OpengGL tutorial.
• People interested in program organization (programming language agnostic).
• Fractal lovers and in particular 3D fractal.
• People interested in user interaction in a functional paradigm.

I had in mind for some time now to make a Mandelbrot set explorer. I had already written a command line Mandelbrot set generator in Haskell. This utility is highly parallel; it uses the repa package¹.

This time, we will not parallelize the computation. Instead, we will display the Mandelbrot set extended in 3D using OpenGL and Haskell. You will be able to move it using your keyboard. This object is a Mandelbrot set in the plan (z=0), and something nice to see in 3D.

Here are some screenshots of the result:

And you can see the intermediate steps to reach this goal:

From the 2nd section to the 4th it will be dirtier and dirtier. We start cleaning the code at the 5th section.

Download the source code of this section → 01_Introduction/hglmandel.lhs

First version

We can consider two parts. The first being mostly some boilerplate². And the second part more focused on OpenGL and content.

Let’s play the song of our people

import Graphics.Rendering.OpenGL
import Graphics.UI.GLUT
import Data.IORef

For efficiency reason³, I will not use the default Haskell Complex data type.

data Complex = C Float Float deriving (Show,Eq)

instance Num Complex where
    fromInteger n = C (fromIntegral n,0.0)
    (C x y) * (C z t) = C (z*x - y*t) (y*z + x*t)
    (C x y) + (C z t) = C (x+z) (y+t)
    abs (C x y)     = C (sqrt (x*x + y*y)) 0.0
    signum (C x y)  = C (signum x) (0.0)

We declare some useful functions for manipulating complex numbers:

complex :: Float -> Float -> Complex
complex x y = C x y

real :: Complex -> Float
real (C x y)    = x

im :: Complex -> Float
im   (C x y)    = y

magnitude :: Complex -> Float
magnitude = real.abs

Let us start

We start by giving the main architecture of our program:

main :: IO ()
main = do
  -- GLUT need to be initialized
  (progname,_) <- getArgsAndInitialize
  -- We will use the double buffered mode (GL constraint)
  initialDisplayMode $= [DoubleBuffered]
  -- We create a window with some title
  createWindow "Mandelbrot Set with Haskell and OpenGL"
  -- Each time we will need to update the display
  -- we will call the function 'display'
  displayCallback $= display
  -- We enter the main loop
  mainLoop

Mainly, we initialize our OpenGL application. We declared that the function display will be used to render the graphics:

display = do
  clear [ColorBuffer] -- make the window black
  loadIdentity -- reset any transformation
  preservingMatrix drawMandelbrot
  swapBuffers -- refresh screen

Also here, there is only one interesting line; the draw will occur in the function drawMandelbrot.

This function will provide a list of draw actions. Remember that OpenGL is imperative by design. Then, one of the consequence is you must write the actions in the right order. No easy parallel drawing here. Here is the function which will render something on the screen:

drawMandelbrot =
  -- We will print Points (not triangles for example)
  renderPrimitive Points $ do
    mapM_ drawColoredPoint allPoints
  where
      drawColoredPoint (x,y,c) = do
          color c -- set the current color to c
          -- then draw the point at position (x,y,0)
          -- remember we're in 3D
          vertex $ Vertex3 x y 0

The mapM_ function is mainly the same as map but inside a monadic context. More precisely, this can be transformed as a list of actions where the order is important:

drawMandelbrot =
  renderPrimitive Points $ do
    color color1
    vertex $ Vertex3 x1 y1 0
    ...
    color colorN
    vertex $ Vertex3 xN yN 0

We also need some kind of global variables. In fact, global variable are a proof of a design problem. We will get rid of them later.

width = 320 :: GLfloat
height = 320 :: GLfloat

And of course our list of colored points. In OpenGL the default coordinate are from -1 to 1.

allPoints :: [(GLfloat,GLfloat,Color3 GLfloat)]
allPoints = [ (x/width,y/height,colorFromValue $ mandel x y) |
                  x <- [-width..width],
                  y <- [-height..height]]

We need a function which transform an integer value to some color:

colorFromValue n =
  let
      t :: Int -> GLfloat
      t i = 0.5 + 0.5*cos( fromIntegral i / 10 )
  in
    Color3 (t n) (t (n+5)) (t (n+10))

And now the mandel function. Given two coordinates in pixels, it returns some integer value:

mandel x y =
  let r = 2.0 * x / width
      i = 2.0 * y / height
  in
      f (complex r i) 0 64

It uses the main Mandelbrot function for each complex \(c\). The Mandelbrot set is the set of complex number \(c\) such that the following sequence does not escape to infinity.

Let us define \(f_c: \)

f_c(z) = z² + c

The sequence is:

0 → f_c(0) → f_c(f_c(0)) → ⋯ → f_cⁿ(0) → ⋯

Of course, instead of trying to test the real limit, we just make a test after a finite number of occurrences.

f :: Complex -> Complex -> Int -> Int
f c z 0 = 0
f c z n = if (magnitude z > 2 )
          then n
          else f c ((z*z)+c) (n-1)

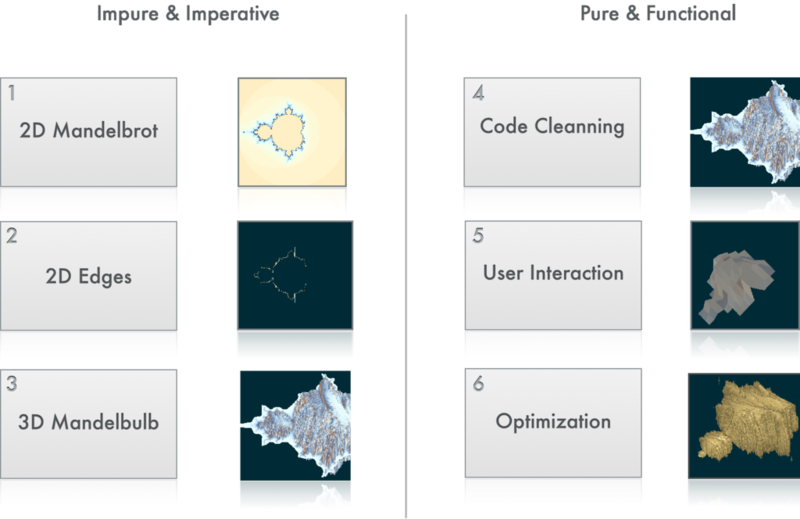
Well, if you download this file (look at the bottom of this section), compile it and run it this is the result:

A first very interesting property of this program is that the computation for all the points is done only once. It is a bit long before the first image appears, but if you resize the window, it updates instantaneously. This property is a direct consequence of purity. If you look closely, you see that allPoints is a pure list. Therefore, calling allPoints will always render the same result and Haskell is clever enough to use this property. While Haskell doesn’t garbage collect allPoints the result is reused for free. We did not specified this value should be saved for later use. It is saved for us.

See what occurs if we make the window bigger:

We see some black lines because we have drawn less point than there is on the surface. We can repair this by drawing little squares instead of just points. But, instead we will do something a bit different and unusual.

Download the source code of this section → 01_Introduction/hglmandel.lhs

Download the source code of this section → 02_Edges/HGLMandelEdge.lhs

Only the edges

import Graphics.Rendering.OpenGL
import Graphics.UI.GLUT
import Data.IORef
-- Use UNPACK data because it is faster
-- The ! is for strict instead of lazy
data Complex = C  {-# UNPACK #-} !Float
                  {-# UNPACK #-} !Float
               deriving (Show,Eq)
instance Num Complex where
    fromInteger n = C (fromIntegral n) 0.0
    (C x y) * (C z t) = C (z*x - y*t) (y*z + x*t)
    (C x y) + (C z t) = C (x+z) (y+t)
    abs (C x y)     = C (sqrt (x*x + y*y)) 0.0
    signum (C x y)  = C (signum x) 0.0
complex :: Float -> Float -> Complex
complex x y = C x y

real :: Complex -> Float
real (C x y)    = x

im :: Complex -> Float
im   (C x y)    = y

magnitude :: Complex -> Float
magnitude = real.abs
main :: IO ()
main = do
  -- GLUT need to be initialized
  (progname,_) <- getArgsAndInitialize
  -- We will use the double buffered mode (GL constraint)
  initialDisplayMode $= [DoubleBuffered]
  -- We create a window with some title
  createWindow "Mandelbrot Set with Haskell and OpenGL"
  -- Each time we will need to update the display
  -- we will call the function 'display'
  displayCallback $= display
  -- We enter the main loop
  mainLoop
display = do
   -- set the background color (dark solarized theme)
  clearColor $= Color4 0 0.1686 0.2117 1
  clear [ColorBuffer] -- make the window black
  loadIdentity -- reset any transformation
  preservingMatrix drawMandelbrot
  swapBuffers -- refresh screen

width = 320 :: GLfloat
height = 320 :: GLfloat

This time, instead of drawing all points, we will simply draw the edges of the Mandelbrot set. The method I use is a rough approximation. I consider the Mandelbrot set to be almost convex. The result will be good enough for the purpose of this tutorial.

We change slightly the drawMandelbrot function. We replace the Points by LineLoop

drawMandelbrot =
  -- We will print Points (not triangles for example)
  renderPrimitive LineLoop $ do
    mapM_ drawColoredPoint allPoints
  where
      drawColoredPoint (x,y,c) = do
          color c -- set the current color to c
          -- then draw the point at position (x,y,0)
          -- remember we're in 3D
          vertex $ Vertex3 x y 0

And now, we should change our list of points. Instead of drawing every point of the visible surface, we will choose only point on the surface.

allPoints = positivePoints ++
      map (\(x,y,c) -> (x,-y,c)) (reverse positivePoints)

We only need to compute the positive point. The Mandelbrot set is symmetric relatively to the abscisse axis.

positivePoints :: [(GLfloat,GLfloat,Color3 GLfloat)]
positivePoints = do
     x <- [-width..width]
     let y = maxZeroIndex (mandel x) 0 height (log2 height)
     if y < 1 -- We don't draw point in the absciss
        then []
        else return (x/width,y/height,colorFromValue $ mandel x y)
     where
         log2 n = floor ((log n) / log 2)

This function is interesting. For those not used to the list monad here is a natural language version of this function:

positivePoints =
    for all x in the range [-width..width]
    let y be smallest number s.t. mandel x y > 0
    if y is on 0 then don't return a point
    else return the value corresonding to (x,y,color for (x+iy))

In fact using the list monad you write like if you consider only one element at a time and the computation is done non deterministically. To find the smallest number such that mandel x y > 0 we use a simple dichotomy:

-- given f min max nbtest,
-- considering
--  - f is an increasing function
--  - f(min)=0
--  - f(max)≠0
-- then maxZeroIndex f min max nbtest returns x such that
--    f(x - ε)=0 and f(x + ε)≠0
--    where ε=(max-min)/2^(nbtest+1)
maxZeroIndex func minval maxval 0 = (minval+maxval)/2
maxZeroIndex func minval maxval n =
  if (func medpoint) /= 0
       then maxZeroIndex func minval medpoint (n-1)
       else maxZeroIndex func medpoint maxval (n-1)
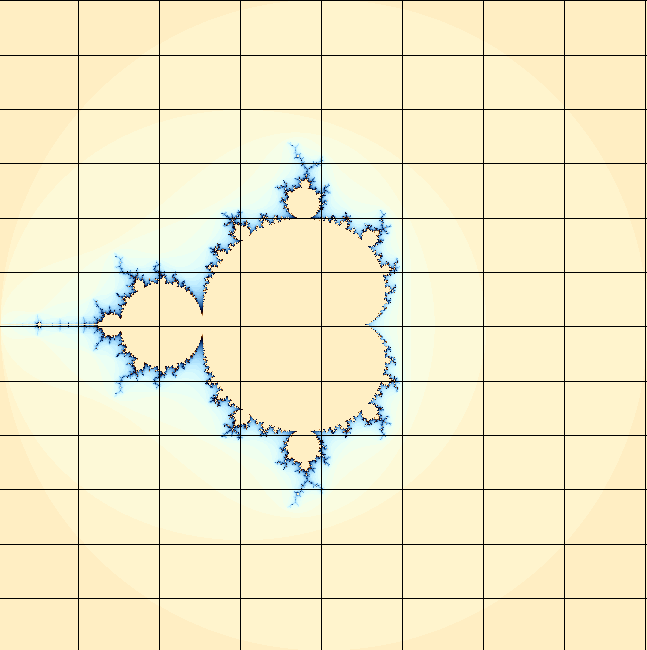
  where medpoint = (minval+maxval)/2

No rocket science here. See the result now:

colorFromValue n =
  let
      t :: Int -> GLfloat
      t i = 0.5 + 0.5*cos( fromIntegral i / 10 )
  in
    Color3 (t n) (t (n+5)) (t (n+10))

mandel x y =
  let r = 2.0 * x / width
      i = 2.0 * y / height
  in
      f (complex r i) 0 64

f :: Complex -> Complex -> Int -> Int
f c z 0 = 0
f c z n = if (magnitude z > 2 )
          then n
          else f c ((z*z)+c) (n-1)

Download the source code of this section → 02_Edges/HGLMandelEdge.lhs

Download the source code of this section → 03_Mandelbulb/Mandelbulb.lhs

3D Mandelbrot?

Now we will we extend to a third dimension. But, there is no 3D equivalent to complex. In fact, the only extension known are quaternions (in 4D). As I know almost nothing about quaternions, I will use some extended complex, instead of using a 3D projection of quaternions. I am pretty sure this construction is not useful for numbers. But it will be enough for us to create something that look nice.

This section is quite long, but don’t be afraid, most of the code is some OpenGL boilerplate. If you just want to skim this section, here is a high level representation:

• OpenGL Boilerplate
  • set some IORef (understand variables) for states
  • Drawing:
    • set doubleBuffer, handle depth, window size…
    • Use state to apply some transformations
  • Keyboard: hitting some key change the state of IORef
• Generate 3D Object

  allPoints :: [ColoredPoint]
  allPoints =
      for all (x,y), -width<x<width, 0<y<height
      Let z be the minimal depth such that
          mandel x y z > 0
      add the points
             (x, y, z,color)
             (x,-y, z,color)
             (x, y,-z,color)
             (x,-y,-z,color)
          + neighbors to make triangles

import Graphics.Rendering.OpenGL
import Graphics.UI.GLUT
import Data.IORef
type ColoredPoint = (GLfloat,GLfloat,GLfloat,Color3 GLfloat)

We declare a new type ExtComplex (for extended complex). An extension of complex numbers with a third component:

data ExtComplex = C GLfloat GLfloat GLfloat
                  deriving (Show,Eq)
instance Num ExtComplex where
    -- The shape of the 3D mandelbrot
    -- will depend on this formula
    (C x y z) * (C x' y' z') = C (x*x' - y*y' - z*z')
                                 (x*y' + y*x' + z*z')
                                 (x*z' + z*x')
    -- The rest is straightforward
    fromInteger n = C (fromIntegral n) 0  0
    (C x y z) + (C x' y' z') = C (x+x')  (y+y') (z+z')
    abs (C x y z)     = C (sqrt (x*x + y*y + z*z)) 0  0
    signum (C x y z)  = C (signum x) (signum y) (signum z)

The most important part is the new multiplication instance. Modifying this formula will change radically the shape of the result. Here is the formula written in a more mathematical notation. I called the third component of these extended complex strange.

real((x, y, z) × (x′, y′, z′)) = xx′ − yy′ − zz′

im((x, y, z) × (x′, y′, z′)) = xy′ − yx′ + zz′

strange((x, y, z) × (x′, y′, z′)) = xz′ + zx′

Note how if \(z=z’=0\) then the multiplication is the same to the complex one.

extcomplex :: GLfloat -> GLfloat -> GLfloat -> ExtComplex
extcomplex x y z = C x y z

real :: ExtComplex -> GLfloat
real (C (x,y,z))    = x

im :: ExtComplex -> GLfloat
im   (C (x,y,z))    = y

strange :: ExtComplex -> GLfloat
strange (C (x,y,z)) = z

magnitude :: ExtComplex -> GLfloat
magnitude = real.abs

From 2D to 3D

As we will use some 3D, we add some new directive in the boilerplate. But mainly, we simply state that will use some depth buffer. And also we will listen the keyboard.

main :: IO ()
main = do
  -- GLUT need to be initialized
  (progname,_) <- getArgsAndInitialize
  -- We will use the double buffered mode (GL constraint)
  -- We also Add the DepthBuffer (for 3D)
  initialDisplayMode $=
      [WithDepthBuffer,DoubleBuffered,RGBMode]
  -- We create a window with some title
  createWindow "3D HOpengGL Mandelbrot"
  -- We add some directives
  depthFunc  $= Just Less
  windowSize $= Size 500 500
  -- Some state variables (I know it feels BAD)
  angle   <- newIORef ((35,0)::(GLfloat,GLfloat))
  zoom    <- newIORef (2::GLfloat)
  campos  <- newIORef ((0.7,0)::(GLfloat,GLfloat))
  -- Function to call each frame
  idleCallback $= Just idle
  -- Function to call when keyboard or mouse is used
  keyboardMouseCallback $=
          Just (keyboardMouse angle zoom campos)
  -- Each time we will need to update the display
  -- we will call the function 'display'
  -- But this time, we add some parameters
  displayCallback $= display angle zoom campos
  -- We enter the main loop
  mainLoop

The idle is here to change the states. There should never be any modification done in the display function.

idle = postRedisplay Nothing

We introduce some helper function to manipulate standard IORef. Mainly modVar x f is equivalent to the imperative x:=f(x), modFst (x,y) (+1) is equivalent to (x,y) := (x+1,y) and modSnd (x,y) (+1) is equivalent to (x,y) := (x,y+1)

modVar v f = do
  v' <- get v
  v $= (f v')
mapFst f (x,y) = (f x,  y)
mapSnd f (x,y) = (  x,f y)

And we use them to code the function handling keyboard. We will use the keys hjkl to rotate, oi to zoom and sedf to move. Also, hitting space will reset the view. Remember that angle and campos are pairs and zoom is a scalar. Also note (+0.5) is the function \x->x+0.5 and (-0.5) is the number -0.5 (yes I share your pain).

keyboardMouse angle zoom campos key state modifiers position =
  -- We won't use modifiers nor position
  kact angle zoom campos key state
  where
    -- reset view when hitting space
    kact a z p (Char ' ') Down = do
          a $= (0,0) -- angle
          z $= 1     -- zoom
          p $= (0,0) -- camera position
    -- use of hjkl to rotate
    kact a _ _ (Char 'h') Down = modVar a (mapFst (+0.5))
    kact a _ _ (Char 'l') Down = modVar a (mapFst (+(-0.5)))
    kact a _ _ (Char 'j') Down = modVar a (mapSnd (+0.5))
    kact a _ _ (Char 'k') Down = modVar a (mapSnd (+(-0.5)))
    -- use o and i to zoom
    kact _ z _ (Char 'o') Down = modVar z (*1.1)
    kact _ z _ (Char 'i') Down = modVar z (*0.9)
    -- use sdfe to move the camera
    kact _ _ p (Char 's') Down = modVar p (mapFst (+0.1))
    kact _ _ p (Char 'f') Down = modVar p (mapFst (+(-0.1)))
    kact _ _ p (Char 'd') Down = modVar p (mapSnd (+0.1))
    kact _ _ p (Char 'e') Down = modVar p (mapSnd (+(-0.1)))
    -- any other keys does nothing
    kact _ _ _ _ _ = return ()

Note display takes some parameters this time. This function if full of boilerplate:

display angle zoom position = do
   -- set the background color (dark solarized theme)
  clearColor $= Color4 0 0.1686 0.2117 1
  clear [ColorBuffer,DepthBuffer]
  -- Transformation to change the view
  loadIdentity -- reset any transformation
  -- tranlate
  (x,y) <- get position
  translate $ Vector3 x y 0
  -- zoom
  z <- get zoom
  scale z z z
  -- rotate
  (xangle,yangle) <- get angle
  rotate xangle $ Vector3 1.0 0.0 (0.0::GLfloat)
  rotate yangle $ Vector3 0.0 1.0 (0.0::GLfloat)

  -- Now that all transformation were made
  -- We create the object(s)
  preservingMatrix drawMandelbrot

  swapBuffers -- refresh screen

Not much to say about this function. Mainly there are two parts: apply some transformations, draw the object.

The 3D Mandelbrot

We have finished with the OpenGL section, let’s talk about how we generate the 3D points and colors. First, we will set the number of details to 200 pixels in the three dimensions.

nbDetails = 200 :: GLfloat
width  = nbDetails
height = nbDetails
deep   = nbDetails

This time, instead of just drawing some line or some group of points, we will show triangles. The function allPoints will provide a multiple of three points. Each three successive point representing the coordinate of each vertex of a triangle.

drawMandelbrot = do
  -- We will print Points (not triangles for example)
  renderPrimitive Triangles $ do
    mapM_ drawColoredPoint allPoints
  where
      drawColoredPoint (x,y,z,c) = do
          color c
          vertex $ Vertex3 x y z

In fact, we will provide six ordered points. These points will be used to draw two triangles.

The next function is a bit long. Here is an approximative English version:

forall x from -width to width
  forall y from -height to height
    forall the neighbors of (x,y)
      let z be the smalled depth such that (mandel x y z)>0
      let c be the color given by mandel x y z
      add the point corresponding to (x,y,z,c)

Also, I added a test to hide points too far from the border. In fact, this function show points close to the surface of the modified mandelbrot set. But not the mandelbrot set itself.

depthPoints :: [ColoredPoint]
depthPoints = do
  x <- [-width..width]
  y <- [-height..height]
  let
      depthOf x' y' = maxZeroIndex (mandel x' y') 0 deep logdeep
      logdeep = floor ((log deep) / log 2)
      z1 = depthOf    x     y
      z2 = depthOf (x+1)    y
      z3 = depthOf (x+1) (y+1)
      z4 = depthOf    x  (y+1)
      c1 = mandel    x     y  (z1+1)
      c2 = mandel (x+1)    y  (z2+1)
      c3 = mandel (x+1) (y+1) (z3+1)
      c4 = mandel    x  (y+1) (z4+1)
      p1 = (   x /width,   y /height, z1/deep, colorFromValue c1)
      p2 = ((x+1)/width,   y /height, z2/deep, colorFromValue c2)
      p3 = ((x+1)/width,(y+1)/height, z3/deep, colorFromValue c3)
      p4 = (   x /width,(y+1)/height, z4/deep, colorFromValue c4)
  if (and $ map (>=57) [c1,c2,c3,c4])
  then []
  else [p1,p2,p3,p1,p3,p4]

If you look at the function above, you see a lot of common patterns. Haskell is very efficient to make this better. Here is a harder to read but shorter and more generic rewritten function:

depthPoints :: [ColoredPoint]
depthPoints = do
  x <- [-width..width]
  y <- [-height..height]
  let
    neighbors = [(x,y),(x+1,y),(x+1,y+1),(x,y+1)]
    depthOf (u,v) = maxZeroIndex (mandel u v) 0 deep logdeep
    logdeep = floor ((log deep) / log 2)
    -- zs are 3D points with found depth
    zs = map (\(u,v) -> (u,v,depthOf (u,v))) neighbors
    -- ts are 3D pixels + mandel value
    ts = map (\(u,v,w) -> (u,v,w,mandel u v (w+1))) zs
    -- ps are 3D opengl points + color value
    ps = map (\(u,v,w,c') ->
        (u/width,v/height,w/deep,colorFromValue c')) ts
  -- If the point diverged too fast, don't display it
  if (and $ map (\(_,_,_,c) -> c>=57) ts)
  then []
  -- Draw two triangles
  else [ps!!0,ps!!1,ps!!2,ps!!0,ps!!2,ps!!3]

If you prefer the first version, then just imagine how hard it will be to change the enumeration of the point from (x,y) to (x,z) for example.

Also, we didn’t searched for negative values. This modified Mandelbrot is no more symmetric relatively to the plan y=0. But it is symmetric relatively to the plan z=0. Then I mirror these values.

allPoints :: [ColoredPoint]
allPoints = planPoints ++ map inverseDepth  planPoints
  where
      planPoints = depthPoints
      inverseDepth (x,y,z,c) = (x,y,-z+1/deep,c)

The rest of the program is very close to the preceding one.

-- given f min max nbtest,
-- considering
--  - f is an increasing function
--  - f(min)=0
--  - f(max)≠0
-- then maxZeroIndex f min max nbtest returns x such that
--    f(x - ε)=0 and f(x + ε)≠0
--    where ε=(max-min)/2^(nbtest+1)
maxZeroIndex :: (Fractional a,Num a,Num b,Eq b) =>
                 (a -> b) -> a -> a -> Int -> a
maxZeroIndex func minval maxval 0 = (minval+maxval)/2
maxZeroIndex func minval maxval n =
  if (func medpoint) /= 0
       then maxZeroIndex func minval medpoint (n-1)
       else maxZeroIndex func medpoint maxval (n-1)
  where medpoint = (minval+maxval)/2

colorFromValue n =
  let
      t :: Int -> GLfloat
      t i = 0.7 + 0.3*cos( fromIntegral i / 10 )
  in
    Color3 (t n) (t (n+5)) (t (n+10))

f :: ExtComplex -> ExtComplex -> Int -> Int
f c z 0 = 0
f c z n = if (magnitude z > 2 )
          then n
          else f c ((z*z)+c) (n-1)

We simply add a new dimension to the mandel function and change the type signature of f from Complex to ExtComplex.

mandel x y z =
  let r = 2.0 * x / width
      i = 2.0 * y / height
      s = 2.0 * z / deep
  in
      f (extcomplex r i s) 0 64

Here is the result:

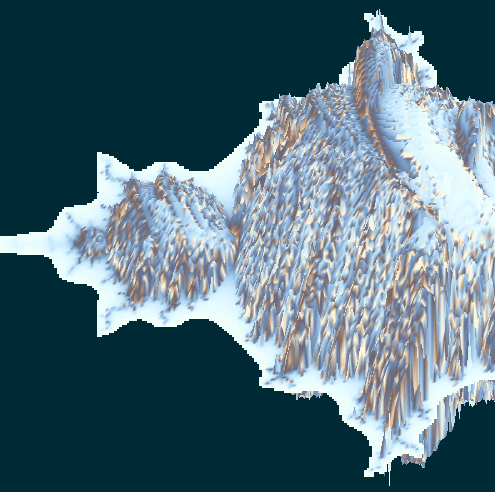
Download the source code of this section → 03_Mandelbulb/Mandelbulb.lhs

Download the source code of this section → 04_Mandelbulb/Mandelbulb.lhs

Naïve code cleaning

The first approach to clean the code is to separate the GLUT/OpenGL part from the computation of the shape. Here is the cleaned version of the preceding section. Most boilerplate was put in external files.

• YBoiler.hs, the 3D rendering
• Mandel, the mandel function
• ExtComplex, the extended complexes

import YBoiler -- Most the OpenGL Boilerplate
import Mandel -- The 3D Mandelbrot maths

The yMainLoop takes two arguments: the title of the window and a function from time to triangles

main :: IO ()
main = yMainLoop "3D Mandelbrot" (\_ -> allPoints)

We set some global constant (this is generally bad).

nbDetails = 200 :: GLfloat
width  = nbDetails
height = nbDetails
deep   = nbDetails

We then generate colored points from our function. This is similar to the preceding section.

allPoints :: [ColoredPoint]
allPoints = planPoints ++ map inverseDepth  planPoints
  where
      planPoints = depthPoints ++ map inverseHeight depthPoints
      inverseHeight (x,y,z,c) = (x,-y,z,c)
      inverseDepth (x,y,z,c) = (x,y,-z+1/deep,c)

depthPoints :: [ColoredPoint]
depthPoints = do
  x <- [-width..width]
  y <- [0..height]
  let
    neighbors = [(x,y),(x+1,y),(x+1,y+1),(x,y+1)]
    depthOf (u,v) = maxZeroIndex (ymandel u v) 0 deep 7
    -- zs are 3D points with found depth
    zs = map (\(u,v) -> (u,v,depthOf (u,v))) neighbors
    -- ts are 3D pixels + mandel value
    ts = map (\(u,v,w) -> (u,v,w,ymandel u v (w+1))) zs
    -- ps are 3D opengl points + color value
    ps = map (\(u,v,w,c') ->
        (u/width,v/height,w/deep,colorFromValue c')) ts
  -- If the point diverged too fast, don't display it
  if (and $ map (\(_,_,_,c) -> c>=57) ts)
  then []
  -- Draw two triangles
  else [ps!!0,ps!!1,ps!!2,ps!!0,ps!!2,ps!!3]

-- given f min max nbtest,
-- considering
--  - f is an increasing function
--  - f(min)=0
--  - f(max)≠0
-- then maxZeroIndex f min max nbtest returns x such that
--    f(x - ε)=0 and f(x + ε)≠0
--    where ε=(max-min)/2^(nbtest+1)
maxZeroIndex func minval maxval 0 = (minval+maxval)/2
maxZeroIndex func minval maxval n =
  if (func medpoint) /= 0
       then maxZeroIndex func minval medpoint (n-1)
       else maxZeroIndex func medpoint maxval (n-1)
  where medpoint = (minval+maxval)/2

colorFromValue n =
  let
      t :: Int -> GLfloat
      t i = 0.7 + 0.3*cos( fromIntegral i / 10 )
  in
    ((t n),(t (n+5)),(t (n+10)))

ymandel x y z = mandel (2*x/width) (2*y/height) (2*z/deep) 64

This code is cleaner but many things doesn’t feel right. First, all the user interaction code is outside our main file. I feel it is okay to hide the detail for the rendering. But I would have preferred to control the user actions.

On the other hand, we continue to handle a lot rendering details. For example, we provide ordered vertices.

Download the source code of this section → 04_Mandelbulb/Mandelbulb.lhs

Download the source code of this section → 05_Mandelbulb/Mandelbulb.lhs

Functional organization?

Some points:

1. OpenGL and GLUT is done in C. In particular the mainLoop function is a direct link to the C library (FFI). This function is clearly far from the functional paradigm. Could we make this better? We will have two choices:

   • create our own mainLoop function to make it more functional.
   • deal with the imperative nature of the GLUT mainLoop function.
   As one of the goal of this article is to understand how to deal with existing libraries and particularly the one coming from imperative languages, we will continue to use the mainLoop function.

2. Our main problem come from user interaction. If you ask “the Internet”, about how to deal with user interaction with a functional paradigm, the main answer is to use functional reactive programming (FRP). I won’t use FRP in this article. Instead, I’ll use a simpler while less effective way to deal with user interaction. But The method I’ll use will be as pure and functional as possible.

Here is how I imagine things should go. First, what the main loop should look like if we could make our own:

functionalMainLoop =
    Read user inputs and provide a list of actions
    Apply all actions to the World
    Display one frame
    repetere aeternum

Clearly, ideally we should provide only three parameters to this main loop function:

• an initial World state
• a mapping between the user interactions and functions which modify the world
• a function taking two parameters: time and world state and render a new world without user interaction.

Here is a real working code, I’ve hidden most display functions. The YGL, is a kind of framework to display 3D functions. But it can easily be extended to many kind of representation.

import YGL -- Most the OpenGL Boilerplate
import Mandel -- The 3D Mandelbrot maths

We first set the mapping between user input and actions. The type of each couple should be of the form (user input, f) where (in a first time) f:World -> World. It means, the user input will transform the world state.

-- Centralize all user input interaction
inputActionMap :: InputMap World
inputActionMap = inputMapFromList [
     (Press 'k' , rotate xdir   5)
    ,(Press 'i' , rotate xdir (-5))
    ,(Press 'j' , rotate ydir   5)
    ,(Press 'l' , rotate ydir (-5))
    ,(Press 'o' , rotate zdir   5)
    ,(Press 'u' , rotate zdir (-5))
    ,(Press 'f' , translate xdir   0.1)
    ,(Press 's' , translate xdir (-0.1))
    ,(Press 'e' , translate ydir   0.1)
    ,(Press 'd' , translate ydir (-0.1))
    ,(Press 'z' , translate zdir   0.1)
    ,(Press 'r' , translate zdir (-0.1))
    ,(Press '+' , zoom    1.1)
    ,(Press '-' , zoom (1/1.1))
    ,(Press 'h' , resize    1.2)
    ,(Press 'g' , resize (1/1.2))
    ]

And of course a type design the World State. The important part is that it is our World State type. We could have used any kind of data type.

-- I prefer to set my own name for these types
data World = World {
      angle       :: Point3D
    , scale       :: Scalar
    , position    :: Point3D
    , shape       :: Scalar -> Function3D
    , box         :: Box3D
    , told        :: Time -- last frame time
    }

The important part to glue our own type to the framework is to make our type an instance of the type class DisplayableWorld. We simply have to provide the definition of some functions.

instance DisplayableWorld World where
  winTitle _ = "The YGL Mandelbulb"
  camera w = Camera {
        camPos = position w,
        camDir = angle w,
        camZoom = scale w }
  -- objects for world w
  -- is the list of one unique element
  -- The element is an YObject
  --   more precisely the XYFunc Function3D Box3D
  --   where the Function3D is the type
  --             Point -> Point -> Maybe (Point,Color)
  --   and its value here is ((shape w) res)
  --   and the Box3D value is defbox
  objects w = [XYFunc ((shape  w) res) defbox]
              where
                  res = resolution $ box w
                  defbox = box w

The camera function will retrieve an object of type Camera which contains most necessary information to set our camera. The objects function will returns a list of objects. Their type is YObject. Note the generation of triangles is no more in this file. Until here we only used declarative pattern.

We also need to set all our transformation functions. These function are used to update the world state.

xdir :: Point3D
xdir = makePoint3D (1,0,0)
ydir :: Point3D
ydir = makePoint3D (0,1,0)
zdir :: Point3D
zdir = makePoint3D (0,0,1)

Note (-*<) is the scalar product (α -*< (x,y,z) = (αx,αy,αz)). Also note we could add two Point3D.

rotate :: Point3D -> Scalar -> World -> World
rotate dir angleValue world =
  world {
     angle = (angle world) + (angleValue -*< dir) }

translate :: Point3D -> Scalar -> World -> World
translate dir len world =
  world {
    position = (position world) + (len -*< dir) }

zoom :: Scalar -> World -> World
zoom z world = world {
    scale = z * scale world }

resize :: Scalar -> World -> World
resize r world = world {
    box = (box world) {
     resolution = sqrt ((resolution (box world))**2 * r) }}

The resize is used to generate the 3D function. As I wanted the time spent to generate a more detailed view to grow linearly I use this not so straightforward formula.

The yMainLoop takes three arguments.

• A map between user Input and world transformation
• A timed world transformation
• An initial world state

main :: IO ()
main = yMainLoop inputActionMap idleAction initialWorld

Here is our initial world state.

-- We initialize the world state
-- then angle, position and zoom of the camera
-- And the shape function
initialWorld :: World
initialWorld = World {
   angle = makePoint3D (-30,-30,0)
 , position = makePoint3D (0,0,0)
 , scale = 0.8
 , shape = shapeFunc
 , box = Box3D { minPoint = makePoint3D (-2,-2,-2)
               , maxPoint =  makePoint3D (2,2,2)
               , resolution =  0.16 }
 , told = 0
 }

We will define shapeFunc later. Here is the function which transform the world even without user action. Mainly it makes some rotation.

idleAction :: Time -> World -> World
idleAction tnew world = world {
    angle = (angle world) + (delta -*< zdir)
  , told = tnew
  }
  where
      anglePerSec = 5.0
      delta = anglePerSec * elapsed / 1000.0
      elapsed = fromIntegral (tnew - (told world))

Now the function which will generate points in 3D. The first parameter (res) is the resolution of the vertex generation. More precisely, res is distance between two points on one direction. We need it to “close” our shape.

The type Function3D is Point -> Point -> Maybe Point. Because we consider partial functions (for some (x,y) our function can be undefined).

shapeFunc :: Scalar -> Function3D
shapeFunc res x y =
  let
      z = maxZeroIndex (ymandel x y) 0 1 20
  in
  if and [ maxZeroIndex (ymandel (x+xeps) (y+yeps)) 0 1 20 < 0.000001 |
              val <- [res], xeps <- [-val,val], yeps<-[-val,val]]
      then Nothing
      else Just (z,colorFromValue ((ymandel x y z) * 64))

With the color function.

colorFromValue :: Point -> Color
colorFromValue n =
  let
      t :: Point -> Scalar
      t i = 0.7 + 0.3*cos( i / 10 )
  in
    makeColor (t n) (t (n+5)) (t (n+10))

The rest is similar to the preceding sections.

-- given f min max nbtest,
-- considering
--  - f is an increasing function
--  - f(min)=0
--  - f(max)≠0
-- then maxZeroIndex f min max nbtest returns x such that
--    f(x - ε)=0 and f(x + ε)≠0
--    where ε=(max-min)/2^(nbtest+1)
maxZeroIndex :: (Fractional a,Num a,Num b,Eq b) =>
                 (a -> b) -> a -> a -> Int -> a
maxZeroIndex _ minval maxval 0 = (minval+maxval)/2
maxZeroIndex func minval maxval n =
  if (func medpoint) /= 0
       then maxZeroIndex func minval medpoint (n-1)
       else maxZeroIndex func medpoint maxval (n-1)
  where medpoint = (minval+maxval)/2

ymandel :: Point -> Point -> Point -> Point
ymandel x y z = fromIntegral (mandel x y z 64) / 64

I won’t explain how the magic occurs here. If you are interested, just read the file YGL.hs. It is commented a lot.

• YGL.hs, the 3D rendering framework
• Mandel, the mandel function
• ExtComplex, the extended complexes

Download the source code of this section → 05_Mandelbulb/Mandelbulb.lhs

Download the source code of this section → 06_Mandelbulb/Mandelbulb.lhs

Optimization

Our code architecture feel very clean. All the meaningful code is in our main file and all display details are externalized. If you read the code of YGL.hs, you’ll see I didn’t made everything perfect. For example, I didn’t finished the code of the lights. But I believe it is a good first step and it will be easy to go further. Unfortunately the program of the preceding session is extremely slow. We compute the Mandelbulb for each frame now.

Before our program structure was:

Constant Function -> Constant List of Triangles -> Display

Now we have

Main loop -> World -> Function -> List of Objects -> Atoms -> Display

The World state could change. The compiler can no more optimize the computation for us. We have to manually explain when to redraw the shape.

To optimize we must do some things in a lower level. Mostly the program remains the same, but it will provide the list of atoms directly.

import YGL -- Most the OpenGL Boilerplate
import Mandel -- The 3D Mandelbrot maths

-- Centralize all user input interaction
inputActionMap :: InputMap World
inputActionMap = inputMapFromList [
     (Press ' ' , switchRotation)
    ,(Press 'k' , rotate xdir 5)
    ,(Press 'i' , rotate xdir (-5))
    ,(Press 'j' , rotate ydir 5)
    ,(Press 'l' , rotate ydir (-5))
    ,(Press 'o' , rotate zdir 5)
    ,(Press 'u' , rotate zdir (-5))
    ,(Press 'f' , translate xdir 0.1)
    ,(Press 's' , translate xdir (-0.1))
    ,(Press 'e' , translate ydir 0.1)
    ,(Press 'd' , translate ydir (-0.1))
    ,(Press 'z' , translate zdir 0.1)
    ,(Press 'r' , translate zdir (-0.1))
    ,(Press '+' , zoom 1.1)
    ,(Press '-' , zoom (1/1.1))
    ,(Press 'h' , resize 2.0)
    ,(Press 'g' , resize (1/2.0))
    ]

data World = World {
      angle       :: Point3D
    , anglePerSec :: Scalar
    , scale       :: Scalar
    , position    :: Point3D
    , box         :: Box3D
    , told        :: Time
    -- We replace shape by cache
    , cache       :: [YObject]
    }

instance DisplayableWorld World where
  winTitle _ = "The YGL Mandelbulb"
  camera w = Camera {
        camPos = position w,
        camDir = angle w,
        camZoom = scale w }
  -- We update our objects instanciation
  objects = cache

xdir :: Point3D
xdir = makePoint3D (1,0,0)
ydir :: Point3D
ydir = makePoint3D (0,1,0)
zdir :: Point3D
zdir = makePoint3D (0,0,1)

rotate :: Point3D -> Scalar -> World -> World
rotate dir angleValue world =
  world {
     angle = angle world + (angleValue -*< dir) }

switchRotation :: World -> World
switchRotation world =
  world {
     anglePerSec = if anglePerSec world > 0 then 0 else 5.0 }

translate :: Point3D -> Scalar -> World -> World
translate dir len world =
  world {
    position = position world + (len -*< dir) }

zoom :: Scalar -> World -> World
zoom z world = world {
    scale = z * scale world }

main :: IO ()
main = yMainLoop inputActionMap idleAction initialWorld

Our initial world state is slightly changed:

-- We initialize the world state
-- then angle, position and zoom of the camera
-- And the shape function
initialWorld :: World
initialWorld = World {
   angle = makePoint3D (30,30,0)
 , anglePerSec = 5.0
 , position = makePoint3D (0,0,0)
 , scale = 1.0
 , box = Box3D { minPoint = makePoint3D (0-eps, 0-eps, 0-eps)
               , maxPoint = makePoint3D (0+eps, 0+eps, 0+eps)
               , resolution =  0.02 }
 , told = 0
 -- We declare cache directly this time
 , cache = objectFunctionFromWorld initialWorld
 }
 where eps=2

The use of eps is a hint to make a better zoom by computing with the right bounds.

We use the YGL.getObject3DFromShapeFunction function directly. This way instead of providing XYFunc, we provide directly a list of Atoms.

objectFunctionFromWorld :: World -> [YObject]
objectFunctionFromWorld w = [Atoms atomList]
  where atomListPositive =
          getObject3DFromShapeFunction
              (shapeFunc (resolution (box w))) (box w)
        atomList = atomListPositive ++
          map negativeTriangle atomListPositive
        negativeTriangle (ColoredTriangle (p1,p2,p3,c)) =
              ColoredTriangle (negz p1,negz p3,negz p2,c)
              where negz (P (x,y,z)) = P (x,y,-z)

We know that resize is the only world change that necessitate to recompute the list of atoms (triangles). Then we update our world state accordingly.

resize :: Scalar -> World -> World
resize r world =
  tmpWorld { cache = objectFunctionFromWorld tmpWorld }
  where
      tmpWorld = world { box = (box world) {
              resolution = sqrt ((resolution (box world))**2 * r) }}

All the rest is exactly the same.

idleAction :: Time -> World -> World
idleAction tnew world =
      world {
        angle = angle world + (delta -*< zdir)
      , told = tnew
      }
  where
      delta = anglePerSec world * elapsed / 1000.0
      elapsed = fromIntegral (tnew - (told world))

shapeFunc :: Scalar -> Function3D
shapeFunc res x y =
  let
      z = maxZeroIndex (ymandel x y) 0 1 20
  in
  if and [ maxZeroIndex (ymandel (x+xeps) (y+yeps)) 0 1 20 < 0.000001 |
              val <- [res], xeps <- [-val,val], yeps<-[-val,val]]
      then Nothing
      else Just (z,colorFromValue 0)

colorFromValue :: Point -> Color
colorFromValue n =
  let
      t :: Point -> Scalar
      t i = 0.0 + 0.5*cos( i /10 )
  in
    makeColor (t n) (t (n+5)) (t (n+10))

-- given f min max nbtest,
-- considering
--  - f is an increasing function
--  - f(min)=0
--  - f(max)≠0
-- then maxZeroIndex f min max nbtest returns x such that
--    f(x - ε)=0 and f(x + ε)≠0
--    where ε=(max-min)/2^(nbtest+1)
maxZeroIndex :: (Fractional a,Num a,Num b,Eq b) =>
                 (a -> b) -> a -> a -> Int -> a
maxZeroIndex _ minval maxval 0 = (minval+maxval)/2
maxZeroIndex func minval maxval n =
  if func medpoint /= 0
       then maxZeroIndex func minval medpoint (n-1)
       else maxZeroIndex func medpoint maxval (n-1)
  where medpoint = (minval+maxval)/2

ymandel :: Point -> Point -> Point -> Point
ymandel x y z = fromIntegral (mandel x y z 64) / 64

And you can also consider minor changes in the YGL.hs source file.

• YGL.hs, the 3D rendering framework
• Mandel, the mandel function
• ExtComplex, the extended complexes

Download the source code of this section → 06_Mandelbulb/Mandelbulb.lhs

Conclusion

As we can use imperative style in a functional language, know you can use functional style in imperative languages. This article exposed a way to organize some code in a functional way. I’d like to stress the usage of Haskell made it very simple to achieve this.

Once you are used to pure functional style, it is hard not to see all advantages it offers.

The code in the two last sections is completely pure and functional. Furthermore I don’t use GLfloat, Color3 or any other OpenGL type. If I want to use another library in the future, I would be able to keep all the pure code and simply update the YGL module.

The YGL module can be seen as a “wrapper” around 3D display and user interaction. It is a clean separator between the imperative paradigm and functional paradigm.

If you want to go further, it shouldn’t be hard to add parallelism. This should be easy mainly because most of the visible code is pure. Such an optimization would have been harder by using directly the OpenGL library.

You should also want to make a more precise object. Because, the Mandelbulb is clearly not convex. But a precise rendering might be very long from O(n².log(n)) to O(n³).